Página Principal (Main)

Introdução

Produção do som

Descrevendo cientificamente um som

Freqüências naturais, harmônicos e sobretons

Criando uma nota musical

Propriedades físicas do som

Como percebemos a mistura de sons

A análise dos sons musicais

Intervalos e raiz harmônica

As escalas musicais

Instrumentos musicais e suas características físicas

Conclusão

Bibliografia

Instrumentos musicais e suas características físicas

Cada tipo de instrumento tem uma espécie de "assinatura", um conjunto de características sonoras associado que, embora possa parecer subjetivo, tem uma descrição matemática extremamente precisa. Anteriormente comentamos que o som pode ser representado pela soma de diversas ondas individuais, que chamamos de componentes de Fourier. O que diferencia um instrumento de outro são as amplitudes e a duração de cada um dos harmônicos presentes no som resultante; a esse conjunto de características chamamos timbre.

A altura de um som está ligada à intensidade com que ele é emitido, ou seja, ao volume sonoro deste som. Em termos físicos, a altura está ligada à amplitude da onda sonora gerada pela vibração de um determinado instrumento ou material. Quanto maior a amplitude da onda, maior é a quantidade de energia que ela carrega, consequentemente, maior é o seu volume.

Entretanto, a altura pode ser também tratada como a "afinação" de um som. Ela é um atributo do sistema auditivo humano a partir do qual sons quaisquer podem ser classificados em uma ordem que vai do mais baixo ao mais alto, como numa escala de notas musicais. A relação entre a altura e a afinação está ligada à freqüência de vibração do objeto que gerou esse som.

As ondas sonoras complexas geradas por um instrumento musical sempre poderá ser representada por uma série de Fourier, compostas das nota fundamentais e da série de harmônicos ou sobretons, cada um com a sua amplitude e fase. A expressão matemática de uma onda complexa poderia ter a seguinte forma:

P = sen w t + 1/2 sen 2w t + 1/3 sen 3w t + 1/4 sen 4w t + 1/5 sen 5w t.

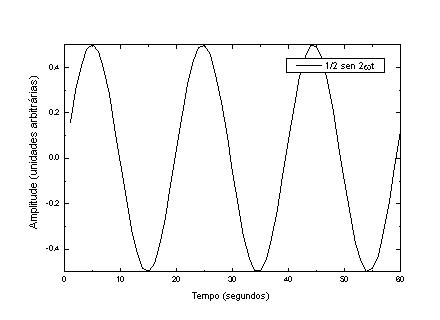
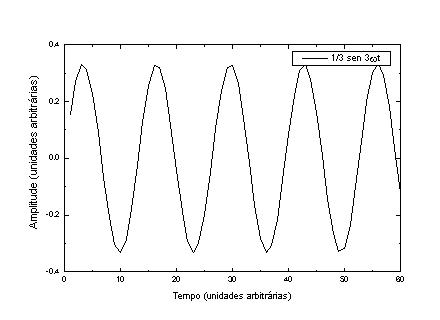
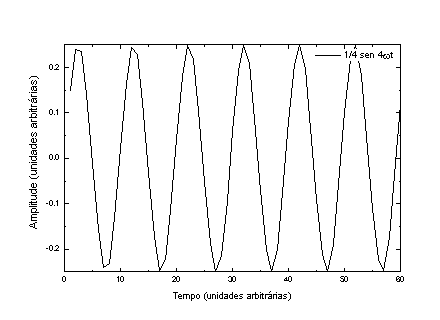
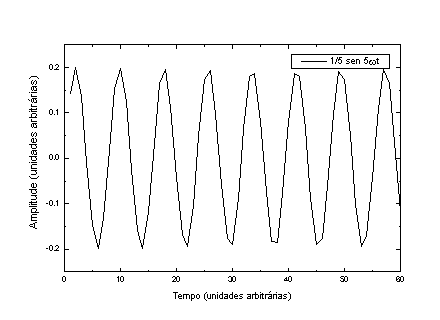
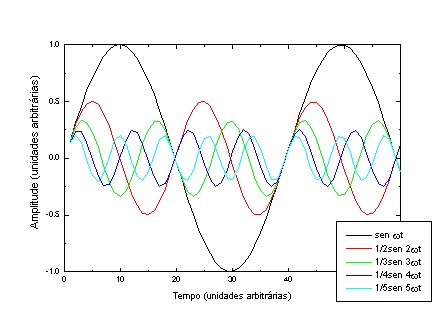
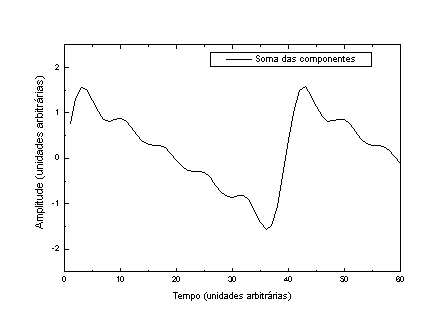
A Figura 4 mostra as componentes individuais e o resultado das somas de todas (P) e da soma de somente os harmônicos ímpares.

a) b)

c) d)

e) f)

g)

Figura 4 – De cima para baixo, as componentes harmônicas da onda representada na página anterior. Em a), b), c), d) e e) temos as componentes individuais, em f) temos todas colocadas na mesma figura e em g) temos a soma das 5 componentes.

A estrutura de uma onda sonora produzida por um instrumento pode ser extremamente complexa. Qual seria o tipo de onda produzido pelas séries abaixo?

P = cos w t + 0,7 cos 2w t + 0,5 cos 3w t                                                                        (5.1)

P = senw t - 0,5sen3w t + 0,33sen5w t – 0,25sen7w t                                                       (5.2)

Figura 5 - Soma dos harmônicos em fase (preto) e em fase invertida (vermelho), de acordo com as equações acima

A fase de uma componente desempenha um papel importantíssimo na determinação da forma da onda resultante. Por exemplo, nas expressões abaixo (vistas na Figura 5) notamos que a fase do terceiro harmônico da segunda expressão está invertida de 180 graus em relação à primeira. Observe como a diferença é notável.

Em geral, exceto por mudança de fases muito grandes, como foi o caso acima, ou sons muito intensos, a fase não é muito importante na determinação da forma da onda.

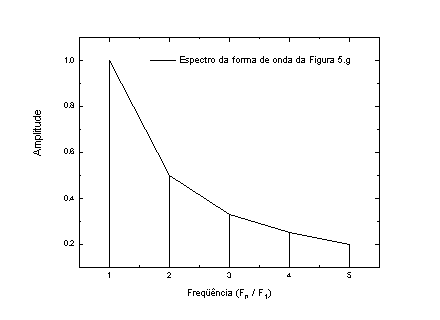
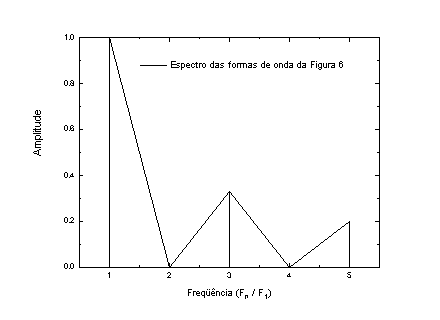
O espectro sonoro é uma forma de mostrar a estrutura de uma onda complexa. Ele é capaz de mostrar quais são as freqüências principais que constituem um determinado som. Então, ao invés de um gráfico onde temos a amplitude em função do tempo, como nas Figuras 4 e 5, teremos um gráfico de amplitude x freqüência. Um exemplo desse gráfico espectral pode ser visto na Figura 6.

O que diferencia um instrumento do outro é exatamente a distribuição de freqüências e das formas de ondas que vimos nas figuras anteriores. Pode-se ver no laboratório que instrumentos de corda são, em geral, bem mais ricos em termos de harmônicos e possuem a forma de onda mais complexa. Os mais pobres são, tipicamente, os de percussão e alguns dos metais (a flauta é o melhor exemplo dos metais, por praticamente não apresentar termos harmônicos de ordem superior a 2, quando ela toca uma nota de freqüência igual a 1568 Hz).

Vamos encerrar esta seção comentando as freqüências fundamentais de ressonância de diversos instrumentos. Elas são características de cada instrumento e dependem, como veremos abaixo, das peculiaridades de cada um. Sistemas acionados por cordas vibrantes possuem uma freqüência fundamental que depende da tensão, massa e comprimento da corda.

Figura 6a – Espectro sonoro da primeira equação dos senos (5.1)

Figura 6b – Espectro sonoro da segunda equação dos senos (5.2)

Membranas vibrantes e discos metálicos, típicos de instrumentos de percussão, possuem um padrão de freqüência fundamental que é típica e parecida uma com a outra, dependendo também da tensão e densidade da membrana. Já tubos sonoros dependem exclusivamente do comprimento da coluna de ar contida no tubo. A Tabela 3 mostra essa relações para diversos ressonadores, inclusive tubos de órgãos metálicos, e a nomenclatura de cada termo. Os termos referentes aos módulos de Young e razão de Poisson podem ser encontrados em qualquer livro texto clássico de Mecânica e oscilações. Os valores são, por uma questão de concordância, dados no sistema de unidades CGS.

Tabela 3 – Relação entre elementos vibradores e suas freqüências de ressonância

(Adaptado da referência 3)